소수란 1과 자기 자신을 제외한 어떠한 정수로도 나눠지지 않는 수를 뜻한다.
프로그래밍을 배우기 시작하고 반복문에 관련된 부분을 배우기 시작하면 문제 / 과제로 많이 나온다.
보통 코딩한 결과는 다음과 같이 나온다.
소수를 구할 최대 숫자 maxNumber, 결과 값을 저장할 result 빈 배열, 1부터 최대 숫자까지 반복문(이하 A), 소수인지 체크하는 isPrimeNumber, 2부터 반복되는 수(A)까지의 반복문(이하 B), A와 B의 나머지 값이 0이면 A는 소수이기에 result에 값을 추가한다.
소수를 구하는 알고리즘 중 에라토스테네스의 체를 이용할 경우 최악과 최선의 코드를 작성 할 수 있다.
에라토스테네스의 체 (Sieve of Eratosthenes)
에라토스테네스의 체는 2에서 부터 maxNumber까지 배열에 넣는다.
- 2를 제외한 나머지 배수를 체크한다.
- 3을 제외한 나머지 배수를 체크한다.
- 5을 제외한 나머지 배수를 체크한다. …
위의 행동을 반복하면 남은 수가 모두 소수가 된다.
코드로 작성하면 다음과 같다. 배수 체크는 0으로 바꾸는 것으로 대체한다.
이렇게 코드를 작성할 경우 소수를 구할 최대 숫자(maxNumber)가 작으면 괜찮지만 많을 경우 오래 걸린다. 실행시간을 체크 할 수 있는 console.time() 함수를 이용하여 측정해봤다.
function getPrimeNumber_1(maxNumber) { ... } // 에라토스테네스의 체
function getPrimeNumber_2(maxNumber) { ... } // 기존 코드
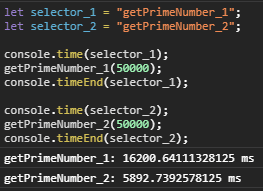
let selector_1 = "getPrimeNumber_1";
let selector_2 = "getPrimeNumber_2";
console.time(selector_1);
getPrimeNumber_1(50000);
console.timeEnd(selector_1);
console.time(selector_2);
getPrimeNumber_2(50000);
console.timeEnd(selector_2);위의 코드로 실행 시간을 따져보면 기존에 만들었던 코드보다 훨씬 느리게 작동한다. 하지만 이런 알고리즘을 잘 활용한다면 최선의 코드를 만들 수 있다.
- 첫번째, 0으로 바뀐 수는 체크하지 않는 것.
- 두번째, 기준 숫자의 배수만 0으로 변경할 것.
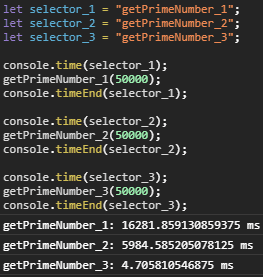
위의 2개의 조건을 적용한 코드는 다음과 같다.
고작 위의 조건을 추가한 걸로 무슨 효과가 있냐고 하겠지만
시간 체크를 해보면 확연하게 차이가 난다.
기존 코드에 누구나 생각 할 수 있는 조건을 추가해보면 엄청나게 개선된 코드를 만들 수 있다.
알고리즘 공부를 열심히 하자.